最近几年中,“紊乱学”(Chaos)异军突起,引起了国内外研究复杂系统的学者的注意。混沌现象与有序现象之间,出现了一座新的桥梁,这就是新发现的普适常数——菲根鲍姆常数。另一方面,对复杂动态系统的研究与计算机绘图技术结合在一起产生了“非整数维几何学”(Fractals),也与紊乱学有密切联系。本文可以说是这类新学科入门的启发性文章,给出的例子实际上指出了混沌现象是怎样在非线性自耦合条件下(Xa+1=f(xn))出现的。原文载H.O.Peitgen. 和P.H.Richter著的“The Beauty of Fractals:Images of Complex Dynamical Systems”一书,Springer-Verlag出版。
——译者
一个人口增长模型
设x0为人口起始值,xn为n年后的人口值,增长率R为每年的相对增长
R=(xn+1-xn)/ xn
如果R为常数r,则动态规律为
xn+1=f(xn)=(1+r)xn (1.1)
n年以后、人口数为xn =(1+r)nx0。为了限制这个指数增长,Verhulst假设增长率R随人口数而变化,为了证明一个给定的生态环境只可能维持一定大小的x值(我们暂且将其定为1),他假定依x而定的增长率R与1-xn成比例,即设R=r(1-xn),常数r>0称为增长参数。由此,如xn<1,则人口数将继续增长,到xn=1时,增长即停。此时动态规律为:
xn+1=f(xn)=(1+r)xn -rxn2 (1.2)
能够使x值不变的x0只有两个:x0=0和x0=1,x0=0时,没有任何东西可以增长。然而,一旦出现一点点机会,使得0<x0≤1,则有r>0,下一年则增长更大。x1=x0+rx0。这样,稳态x0=0是不稳定的。序列x0,x1,x2,…将一直增至其值达到1。为了决定x0=1是否稳定,我们分析增量δn=xn-1是如何依时间而变。把(1.2)式线性化后有:
δn+1=(1-r)δn (1.3)
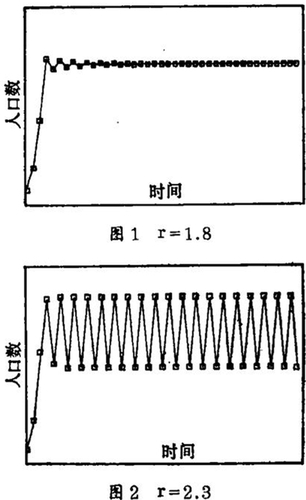
显而易见,当0<r<2时δn+1的绝对值比δn小。图1表明了当r=1.8,x0=0.1时的情况。变化开始时x值增长很快,因为其初始值远小于1,到第三个周期时x值超出了1。根据(1.3)式,δn+1=-0.8δn,增量的绝对值逐渐变小,直到最终落在x=1的状态止,然而,对于r>2,(1.3)式预报出一个增长的δn,其结论是原先的稳态x=1变得不稳定了。图2表示了当r=2.3时。过程变为某两个值之间周期振荡的情况。这使我们考虑到式(1.2)的第一个重复态,xn+2=f(f(xn))= f2(xn),并分析f2的这些固定点(fixed points)的稳定性。我们发现只要r<√6=2.449,这些点都是稳定的。
从有序到紊乱的转变
随着r的增大,分析变得越来越难。对于r=2.5,图3表示出研究过程出现了以4为周期的稳定振荡,进一步的实验发现,越来越小的r值的增加导致新的稳定振荡的周期倍增。最后,在r=2.570时,这个过程就根本没有周期性了。x值不断地在无穷多个可能的值间跳跃,这个过程实际上是决定论的,但却是在长时间内不可预测的。紊乱这个词据此就可以用以来描述这种行为、作为一个例子,图4所示为我们在r=3.0和x0=0.1时获得的结果。
如rn是第n个分叉点处的增长参数,(在这种分叉点上周期、2n变为不稳定,而周期2n+1出现稳定性),则前后两个分叉期间隔的度之比
δn=(rn-rn-1)/ (rn+1-rn)
已被S. GroBmann和S. Thomae,同样被M. Feigenbaum发现是趋于一个常数
δn→δ=4.669… 当n→∞ (1.4)
Feigenbaum实验还指出,不仅在上述维赫斯特过程(Verhulst)中,而且在许多其他类型的过程中都存在这同一个数δ。事实上,δ是一个普适的表达了存在于许多单向过程中的周期倍增现象的特征数。(现称菲根鲍姆常数——译者注)
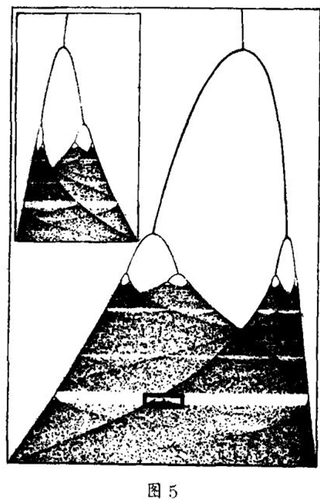
我们当然再乐于介绍几种不同情况下的维赫斯特过程。图(5)是一幅分叉图,它表明了取决于r的(以任意初始值开始的)“渐近动态现象”(asymptotic dynamics)。对每个给定的r值执行5000次个周期重复运算使过程稳定在其“吸引子”(attractor)上(即使过渡过程的特点消失的渐近稳定行为)。然后又做了120个周期的运算以显示吸引子的特性。在r<2时是一点,在2<r<√6时两点,然后4、8、16…点,直到进入紊乱区,吸引子填满了一整条带区。
E. N. Lorenz观察到的在紊乱点r=2.570之前的分叉的瀑布在这一点之后具有相应的结构。这首先是由西德马伯格大学的Siegfried GroBmann和Stefan Thomae指出的:在接近r=3.0时只有一条紊乱带,在r=2.679时分叉为两条带,在r=2.593时叉为四条,然后8、16、32等等,直到r=2.570时这种倍增成为不确定的次数。
图(5)包括了另外的一半分叉树,同样具有由δ刻划的特征,在紊乱区中间我们可以看到吸引子又由可辨别点组成,例如在r=2.8284时出现了一个稳定的周期3,然后又倍增为6、12、24,在r=2.8495时又消失在混沌之中。
读者欲了解更为详细的情况。我们推荐R L De vaney [Del] 和H. G. Schuster的著作。