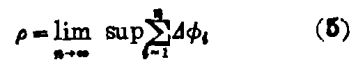浑沌的心律

发布时间：90年05月25日

编译方兆烓

近30年来心律失常的研究达到了新水平，人们可以直接探测单个心肌细胞内的电活动，并借助于心电图及电子计算机自动计测等现代化技术手段使临床观察达到高度精确的水平；因而对心律失常发生机理的研究已进入到亚细胞的层次。

心律失常是一个常见的重要临床症状，它也可以出现于健康人体的心脏中，因而这种不规则性是否一定就是失常，是一个值得考虑的问题。

一些数学家和物理学家近年来对复杂系统的非线性现象的动力学研究的兴趣大增。“浑沌”（Chaos）一词就是他们用来表示确定性方程中的一类动态的；这类状态的演变在时间上是非周期的，而且对初始条件十分敏感。在心律研究中早就出现过“浑沌心动”（Chaotic heart action）一词（见1943年出版的L. N. Katz《心电图学》第2版））。不过，当时心电图专家使用‘浑沌’一词是纯粹描述性的，并不反映对所属机构的详细理论分析。L. Glass等人对胚胎的雏鸡心脏（embryonic chick heart）的自发搏动细胞的周期性电刺激效应进行了实验研究。他们将在此实验系统中观测到的不规则动态用由有限差分方程的分叉理论所得到的理论结果来解释。发现实验系统中所观察到的许多心律与在心电图中临床观察到的异常心律一模一样，因而推测临床观察到的“浑沌”心律可能确实是与无损人体心脏数学模型中的确定性“浑沌”有联系的。

心脏在无外来刺激的条件下，具有自发地、有规律性地发生激动的能力，从而保持心脏有节奏地搏动，在心脏的特化传导系统中，大部分细胞都具有自律性，即为起搏细胞，在正常情况下，窦房结（SA结）是心脏的起搏点，它有节律地产生激动（平静时每分钟60 ~ 100次），从SA结，心脏的活动顺序地普及整个心房肌，使之兴奋收缩，继之心房舒张；在心房收缩的同时，激动传至心房与心室之间的房室结（AV结），再通过特殊的传导组织到心室。所以心房和心室的收缩是顺序发生而不是同步发生的。在心房开始舒张的间时心室肌兴奋收缩，然后心室舒张，房缩与室缩间相隔0.08 ~ 0.12秒，和心搏相关的电化学事件（例如除极与复极）可以在心电图（ECG）上得到监测，它是人体表面不同点间电位差的记录。ECG上有明显特征的偏折或波动都是和心房与心室的激动相联系的_这些波形和时限反映了心房和心室激动的起始部位以及心脏电活动的传导途径。因此‘心电图描记’为诊断和研究复杂的异常心律提供了方便可靠的方法。异常心律心电图的分析不仅有重要的临床意义，它常可对治疗起指导作用，而且也有重大的理论意义。

上面提到的被称为‘浑沌心动’的异常心律，一般认为是由于位于窦房结以外不同区域的多重起搏灶（称为‘异位灶’，ectopic foci）引起的结果。由于从这类异位灶扩展开的电活动的相互作用导致心室经常过早地收缩，在这类情况下ECG上的表现极其复杂而且不规则。当代的研究者们有时仍旧沿用‘浑沌心律’一词来表示多灶的心房与心室心律，临床数据充分表明呈现这类复杂心律的病员有严重的预后。在猝死以前的ECG记录中经常观察到心室的异常心律呈现多种形式的期外收缩（可能由于多重灶引起的）。若为‘浑沌心动’构造一个假设机构的理论模型就必需假定在一个具有复杂形态的易激动的媒质（心肌）中有若干各自独立的起搏点（异位灶），随后对这样一个系统的时间演变进行分析。

目前不打算分析这个困难问题，先来研究一个高度简化的模型系统，它是将一个电子刺激器与一个独立的心脏振荡器单向地耦合。

理论概述

周期扰动与圆映射分叉 范 · 德 · 鲍尔（van der Pol）和范 · 德 · 马克（van der）（Mark）在早期的—篇文章中就提出可以用耦合的非线性振荡器来模拟心律。改变振荡器的相对频率有可能复制出多种不同的心律异常。然而要从数学上去分析他们提出的原始方程是极其困难的，并且后来的研究者已经进行了计算机模拟来确定此动力学。这就使得L. Glass等人考虑给一个天然的心脏振荡器周期地提供短暂的脉动刺激的效应，在下面要提到的某些完全明确的近似下，考虑圆映射可以分析这些情况中的动力学。

假定一个心起搏点的动态可以用常数分方程du/dt=f(y)表示，其中y∈Rⁿ，而f是描写随时间演变的非线性函数。一个具有周期T₀的稳定的极限环振荡给出心的振荡。将环上某点取作y(0)，一般取为动作电位的除极化或上行运动，并将环上任意点y(t)的位相Φ（0≤Φ＜1）定义为t/T₀(mod. 1)。在t→∞的极限下渐近地趋于极限环的所有点的轨迹称为此极限环的吸引流域（basin或‘洼’）。以y(t)，y'(t)代表此吸引流域中两点的轨线，则若lim d [y(t)，y'(t)]=0，其中d为欧几里得距离，y(0)和y'(0)便有相同的终相。具有相同终相的诸点构成的轨迹称为一个同时线（an isochron）。

在某相Φ时发出一个刺激的效果是使振荡器移至相空间内一个具有终相Φ'的新点：

Φ'=g(Φ) （1）

称p为相变曲线（以下以PTC表示）。PTC可以实验测定。在Φ相时给系统发出一个刺激，造成一个长度T的受扰坏。倘若回复到极限环非常迅速，则

g(Φ) =1+ Φ－T/T₀（2）

在回复到极限环并不迅速或振荡器被关断在其吸引流域之外的情况中，（2）式是不适用的。

现在考虑刺激之间间隔为t_s的一个周期性刺激序列的效应。假设在每次刺激之后接着有一个迅速的弛豫返回到极限环，并且假定刺激并不改变系统的内在特性。那么，若Φ_i是第i次刺激以前振荡器的位相，则

Φ_i+1=f(Φ_i)= g(Φ_i)+ τ （3）

其中τ=ts/T₀。（3）式确定一个圆映射。

（2）式和⑶式便是理论研究的基本方程。PTC可以由（2）式实验确定，随后将（3）式作数值的迭代来计算期望的动态。（3）式的稳定点对应于稳定锁相动态^[*]，其中存在一个由N次刺激和心振荡器的M环组成的稳定重复模式锁（N：M锁相），因为PTC是一个将单位圆映射为自身的函数，所以（3）式的分叉分析需要双参数圆映射分叉的知识。τ是一个参数，物理上对应于刺激的周期；另一个参数则是反映通过微电极的扰动电流的强度（包含在PTC中）。下面就近几年来对双参数圆映射的研究中，特别和“浑沌”动力学的实验观察相关的几个主要发现，作一简述：

考虑（3）式所给的映射，定义

?Φ_i= g(Φ_i)+ σ－Φ_i（4）

则旋转数ρ为

ρ对于有限差分方程的环是有理数，因而对于稳定锁相也是有理数。PTC的拓扑度数（topological degree）是计算当Φ绕单位圆一次g绕单位圆的次数。Winfree（1980）曾经举例证明，对小幅度刺激，PTC—般具有度数1；对较大的刺激幅度具有度数0。对度数1的单调圆映射，ρ为无理数时发生准周期动态。若圆映射的临界点是某环上的一点，则此环将是稳定的，称为超稳环。

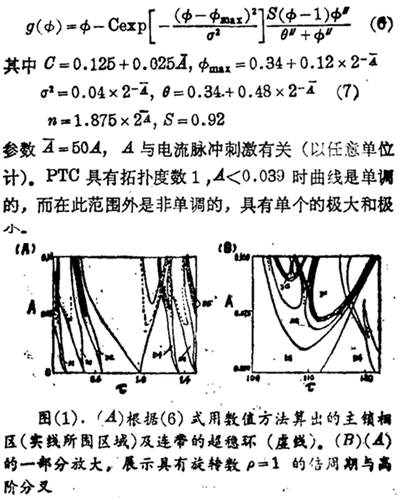
我们采用一个拟合实验数据的PTC来展示从理论上算出的锁相区。此PTC为

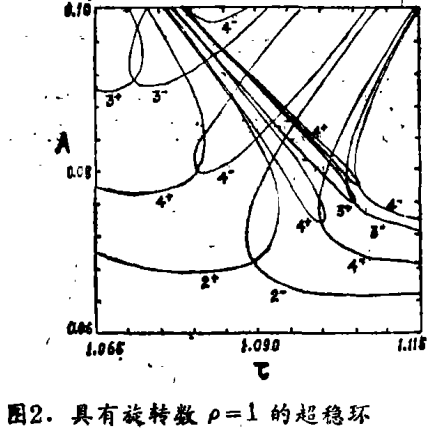
图1为根据（6）式数值计算的主锁相区（实线包围的）和连带的超稳环（虚线），图2所示为旋转数ρ=1的超稳环，它是参数空间更窄的一个局部。图1图2的许多特性已得到充分了解。这些特性，当有从单调性到非单调性的变化时，在任何度数为1的圆映射的分叉中也是可以期望产生的。

圆映射中通向浑沌的路 在图1所示频率 - 振幅参数空间的不同区域内可以观察到不少‘通往浑沌的干线’这里简述其三，即间隙性，倍周期分叉，以及准周期性（共振的重迭），并且证明所有这三条通路在圆映射双参数空间中都能找到：

（ⅲ）准周期性（共振的重迭）准周期动态和PTC单调区内的无理旋转数有关。在此情况中，与任何给定的无理旋转数相关的点的轨迹是一个从A=0伸展到A=0.39的曲线。对于PTC非单调的区域，存在一个楔形区，在其中可以发现某个初始条件是和任一给定的无理旋转数有关的。这个锲形区的产生是Arnold舌的重迭（导致双稳性）以及旋转数复盖非单调圆映射中的一个区间的行为的直接结果。

实验观察结果

在制备好的自发搏动的胚胎雏鸡心细胞团（aggregates）上将一个短暂的电流脉冲通过胞内的微电极使它们受到电刺激。实验的结果在1982 ~ 1984年间有详细的报告，这里只能简单介绍有关浑沌的几个实验观察结果。

在固定的电流幅度下，随着刺激频率降低，在某些频率处观察到周期性的节律而在另一些频率时观察到非周期性的动态。在制备的所有样品中容易看到覆盖参数空间最大面积的周期性节律，2：1，1：1及2：3的节律，并且可以长期保持。在其它一些图形中可以观察到锁相动态（Phase-locked dynamics），但是可以取得的不同图形数目随样品各自的制备和刺激的强度而异。通常，轨道的周期（数字）愈大从实验上去观察它就愈为困难。

若使刺激强度保持不变，观察在不同刺激频率下的两个不同的稳定节律，然后用中间刺激频率来测试，则往往有可能获得非周期性的动态。观察到非周期性动态的参数范围随刺激的频率和振幅而异。

现在就根据前面讨论过的圆映射内的浑沌动力学来解释实验上观察到的这些不规则心律。特别是，从实验上可以观察到前述的三条通往浑沌的路：

（ⅰ）间歇性图1中1：1环带（zone）的高频界对应于一个正切分叉。在1：1带处开始增加刺激频率，最后产生一种情况，其中存在偶然的脉搏短绌（dropped beats）。这些脉搏短绌出现于近似相等的时间间隔上，但图形是不规则的（图3）。理论上预期这种间歇性脉搏短绌存在于一个有干扰系统（noisy systems）中的正切分叉附近。

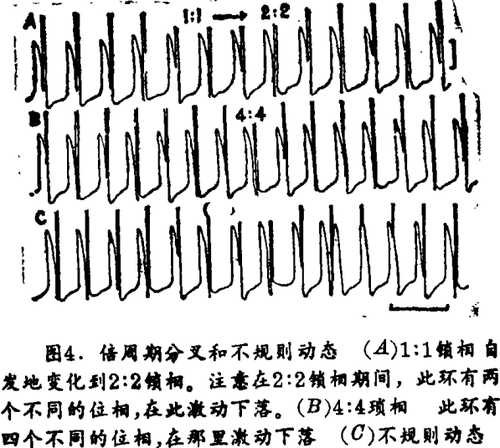
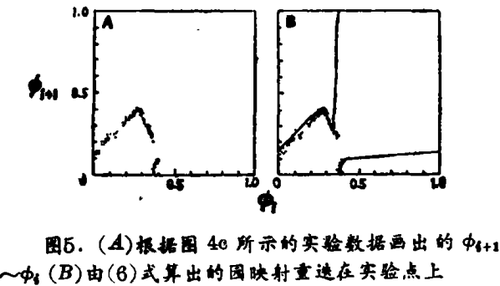
（ⅱ）倍周期若刺激强度充分大（但不是太大），则随着降低刺激频率，料到有从1：1带内部发出的倍周期分叉（图4）。图5a是利用那些取得图4c序列的实验数据测得的和Φ_{i +1} ~ Φ_i图。将根据（6）式得到的PTC曲线所描出的Φ_{i +1} ~ Φ_i（即圆映射）重迭在这些数据上，如图5b所示。可见，由周期性刺激得出的实验数据（点）与以单脉冲干扰实验为基础取得的曲线（实线）之间符合得很好。这就给上节描述的理论以有力支持。

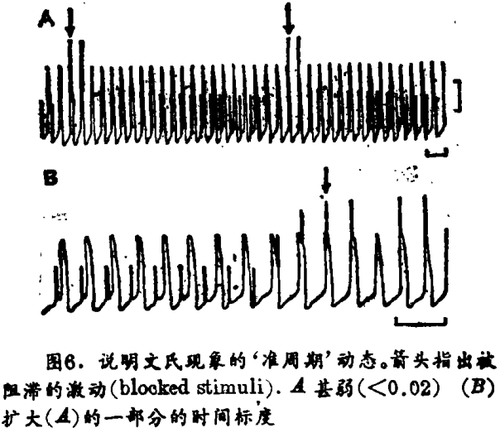
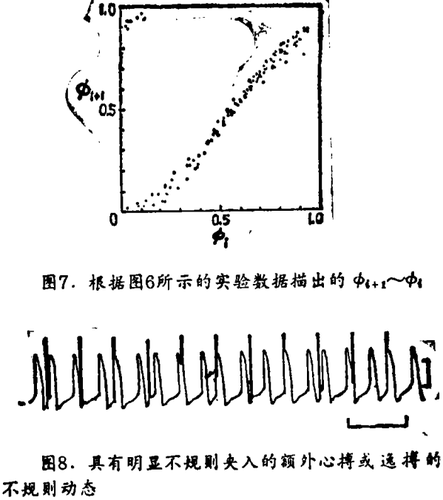
（ⅲ）准周期性在弱刺激强度时诱导带（the zones of entrainment）窄，难以取得稳定的锁相。图6为所得的准周期动态的典型描述，实验测得的Φ_{i +1} ~ Φ_i图为一单调圆映射，差不多是根45°的直线（图7）。因此周期性电刺激几乎没有干扰正在进行的自发心律。

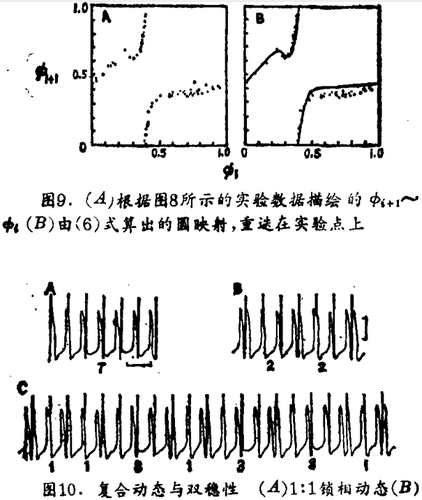
在中等刺激强度时应当由度数1的非单调圆映射来描写动态。图8显示了不规则动态，而图9为此时从实验测得的Φ_{i +1} ~ Φ_i，并将由（2）式的PTC得到的曲线迭在上面，这种情况的动态和在弱刺激强度相同刺激频率时实验观察到的动态（至少在定性上大致看来）没有明显不同，的确，在圆映射正好变为非单调的临界强度的上下，在实验上观察到的动态之间没有鲜明的定性差别。假说：不能从实验上观察到这类差别是由于少量噪声所致，它们破坏了高阶共振在由单调性到非单调性的转变点附近重迭。

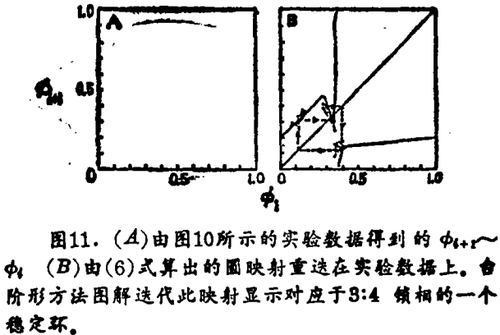
在大的刺激强度时，因为低阶共振重迭，对动态的影响预料会突出些。Glass等人认为图10中的复杂动态是在一个有干扰的系统中共振重迭结果所产生的双稳性的明证。Φ_{i +1} ~ Φ_i图和拟合的PTC（图11）提供了支持此假说的证据。

小结

看来，由胎鸡心脏的周期搏动细胞的周期性刺激导致各种各样规则的和不规则的动态，可以根据1 - 维圆映射分析用理论来分析这个实验，理解这些结果，用这个模型系统来解释若干规则和不规则的心律，它们可以是由于周期性扰动（periodic forcing），来自SA结的冲动，或者AV结或心室组织中的次级节律点所引起的 · 实验上观察到的大量心律实际上在临床观察到的所有心律异常中都有对应。

在无损人体心脏中会发生更其复杂的情况。例如，两个起搏点之间可能有相互作用，因此各自的活动起着重新调整对方的作用。在这种情况下动力学理论分析已证明有大量规则和不规则动态的可能性，对一个可激的但并非自发的振荡媒质的周期刺激产生的‘浑沌’动态的存在也已有人研究。