空间和时间内的“蛀洞”突然成为人们注意的焦点。大蛀洞或许能用作时间装置,小蛀洞或许能确定所有自然常数的值。
过去几年对被理论物理学家称为“蛀洞”的兴趣激增。在空间和时间的几何结构中有许多孔道,连接着宇宙遥远的、完全隔绝的区域。事实上,激发人们兴趣的是两个几乎不相关的课题,一种是宏观蛀洞,就是科幻小说作者或高级文明足以在宇宙遥远距离做空间旅行的那种孔道。另一种是微观蛀洞,其尺度比原子核大约小20个数量级。在这样的尺度上,空间和时间将服从量子物理法则而不是经典定律。
不论哪种类型的蛀洞都是新的概念。理论工作者知道有大尺度蛀洞已有70多年一从爱因斯坦提出引力与时空几何有关的广义相对论之后不久算起。物理学家推测微观蛀洞在认识基本粒子结构,发展引力的量子理论方面能起关键作用也已有30年。然而近来研究工作者发现,这两类对象可能具有某种惊人的,以前从未料想到的特性。大尺度蛀洞或许能提供比较容易的手段向时间反方向行进,尽管由此而带来很多潜在的困难。微观蛀洞或许能通过它们对宇宙量子力学所起的作用,确定所有物理定律中的所有常数的值。许多蛀洞的著作是纯理论的,有些还有很大的争议,但这正是这些课题近来如此吸引人的原因。
1985年加利福尼亚理工学院的迈克尔 · 莫里斯和于尔维 · 尤特塞弗(Ulvi Yurtsever)以及他们的哲学博士论文导师基普 · 索恩,发现大尺度蛀洞新的特征。他们试图用蛀洞的概念充实星际空间旅行,就像卡尔 · 萨根的小说《接触》所描述的那样。他们问道,已知的物理定律要为此做些什么呢?
经典的大尺度蛀洞为爱因斯坦广义相对论场方程的一个解,一种空间和时间几何结构,在该结构中宇宙的两个区域是由短而窄的“咽喉状部分”相连接。最著名的这种几何结构为1916年卡尔 · 施瓦兹奇尔德(Karl Sohwarzschid)发现的球对称的无物质解。这个解的一个区段,略去外部区域之一和咽喉状部分,可用来描述球形的、非转动的恒星,行星和其它物体周围的时空,稍大一些的区段描述非转动的电学上中性的黑洞,但两种情况都没有把宇宙遥远的区域联系起来,只有完整的蛀洞几何结构才能做到这一点(见图1)。
然而不要误解图1。蛀洞并非是静态结构;它表示的是咽喉状部分膨胀到最大的那一瞬间空间的形式。施瓦兹奇尔德蛀洞实际上由零半径膨胀到图1所示的最大半径,然后又收缩回零。此过程进行得极快,哪怕是以光速运动的旅行者也无法从这一孔口穿过蛀洞到另一孔口。这样的蛀洞是无法“通过”的。任何从周围空间掉进蛀洞的物质都促使其收缩,以致旅行者不可能接近并开通一安全通道。
爱因斯坦方程的其它蛀洞解——例如电学上带电的或转动中的黑洞——即使表面上它们是可以通过的,但也有同样的问题。任何掉进蛀洞的物质,或任何辐射,都会被洞的引力场集中和加强到这种程度,致其自身引力会改变时空并使洞封闭。而且,所有这些蛀洞施加的潮汐引力和同样大小的黑洞施加的一样强;以米计或以千米计的混,会在人类大小的旅行者接近它以前很久就被它撕成碎块。显然,适合于空间旅行的洞需要做某些新奇的修饰。
来自加利福尼并理工学院的研究小组构思了可通行蛀洞的几何结构,其咽喉部保持开放,旅行者遇到的只是适度的加速度和潮汐力。广义相对论方程会告诉他们需要何种物质和能量以组成这种蛀洞。他们发现这种洞的咽喉部分必须由具有巨大负压的物质或场穿过,换言之,这种物质要有拉力,有点像被拉长的弹簧。
直径约为1千米的洞,其拉力强度大小和中子星(质量与太阳相当,体积只有地球上高山那么大的一种恒星)中心的压强大小差不多。洞越小,拉力强度越大。最关键的是,拉力强度必须大于物质自身单位体积的能量(即能量密度)。
具有这种特性的物质称为“奇异的”(“exotic”)。我们熟悉的物质,其拉力强度与压力强度远小于能量密度:例如钢的破坏拉力强度大约比它的能量密度小12个数量级(1012倍)。拉力强度大于能量密度意味着某些观察者——相对于蛀洞迅速运动着——将观测到具有负能量密度的物质。爱因斯坦的广义相对论在一组观测者和另一组观测者所测得的能量密度与压强或拉强之间建立了关系。这关系保证,如果对任何一个观测者压强或拉强小于能量密度,那么对所有的观测者能量密度都是正的而不会有负的。爱因斯坦的场方程表明,任何可通行的蛀洞一定含有某种形式的这种奇异物质。
我们还不知道这种要求是不是排除了可通行蛀洞存在的可能性。物理学家一般假设物质服从某种能量条件,其中包括要求所有的观测者测出的全是正的能量密度。然而也存在这些条件靠不住的情况。
例如,两金属板之间的电磁场就能产生负的能量密度。因为按量子力学,电场和磁场服从海森伯测不准原理,它们不断起伏变化,没有精确的经典值。即使在真空中也有这种场的起伏变化。两导电板之间场的起伏能量实际上小于在自由真空中的能量;就是说,它是负的,这种效应以荷兰物理学家亨德里克 · 卡西米尔命名,他在1948年做了计算,并在实验室中得到证实。
剑桥大学的斯蒂芬 · 霍金(Stephen Hawking)于1974年发现的黑洞蒸发,也涉及负的能量密度。
没有人知道制造可通行蛀洞所需要的那种密度和广度的奇异物质是否能存在。如果能存在,如果它和其它物质的相互作用很弱,不会伤害旅行者,或者它被限制在蛀洞中旅行者的通道之外,那么可通行的蛀洞就有存在的可能性。
还有其它理论工作者的研究结果支持这一观点,圣路易斯华盛顿大学的马特 · 维瑟已经找到一种没有危险的蛀洞,旅行者通过它不会遇到任何奇异的或非奇异的物质,丝毫不会感觉到任何力的作用。他取两个叫做闵可夫斯基时空——这是一种无限的,没有任何物质或引力场的真空时空——的复制品,从每一个都挖除同样的区域,并把它们在切口边缘连接起来。边界面上——即现在蛀洞的咽喉部分——的能量密度和压强由爱因斯坦的场方程规定,如果连接面是立体形,那么所有的奇异物质只限于“支持”在立体形边缘上。旅行者便能从一个闵可夫斯基区域穿过立体形表面到另一个区域,而不会和任何物质或力相接触。维瑟的著作还提到,像这样的蛀洞可以造得很稳定——它们既不会坍缩,也不会爆炸,显然各种不同的要求都是为了使蛀洞适于旅行。
有类似想法的还有泰恩河畔纽卡斯尔大学的伊恩 · 英斯、费利西蒂 · 梅勒和保罗 · 戴维斯新近的著作,他们指出,在我们的膨胀宇宙中某些蛀洞可能并没有因落入物质与辐射而引起塌缩。认为我们膨胀宇宙中的蛀洞就是在假想的平滑时空中打的洞并不存在什么问题。
蛀洞作为时间装置
最令人惊奇之处在于,如果物质定律果真允许蛀洞适合于空间旅行,那么它们也就提供了时间旅行的简单手段。把蛀洞的一个洞口固结于遥远的恒星,同时移动另外一个洞口,蛀洞便能成为一时间装置。(从外边看,蛀洞口就是普通的引力物体。你能用另一个物体的万有引力移动它,或者让它带电,用电场移动它)。固结于移动洞口的时钟逐渐慢于静态洞口时钟;它们相对于遥远时钟有“时间膨胀”效应,众所周知这是一种狭义相对论所预测的效应。它们通过蛀洞保持了与静态洞口时钟的联系。
当时钟读数为12:00时从移动中的洞口进入蛀洞,你会在静态洞口出现,那里的时钟读数刚过12:00. 动态洞口时间膨胀的积累使得逆时间旅行成为可能,终于,你能从静态洞口朝动态洞口旅行,穿过中介空间,并在时钟读数比你离开静态洞口还要早的时候到达动态洞口。穿洞返回静态洞口,你到达出发点的时间比你离开的时间要早(见图2)。你已经完成了一次长途旅行,穿过蛀洞,逆时而行。
这并非科幻小说中不受限制的时间旅行。在蛀洞时空内有一面层,其定义,如图2所示,为首次没有花费时间的往返旅行,在此之前不能有逆时间旅行发生。只要处于此界面之外的时空,通过时间往返就是可能的,因此我们必然而临与时间旅行相关的所有佯谬,即重新评估我们所熟悉的因果性和时间演变的概念。
因果性观念——原因先于效果,过去决定现在和将来,等等——已深深扎根于科学思想中。来自加利福尼亚理工学院的研究小组,与莫斯科空间研究的艾戈尔 · 诺维考夫,还有其它物理学家正在合作,检验蛀洞时间装置这些概念的含意。他们用相容性原理补充因果性:物理系统的演变不应自相矛盾,即使你把未来作用的逆时间影响包括在内。这就意味着,如果你逆时间旅行并试图向你诞生以前的父母射击,那么你的武器没发火或者未命中;事件的结果已经包含了你的企图所取得的效果。
研究工作者发现,蛀洞时空简单的“自由”区域,是从蛀洞时间旅行边界线以前的任何初始条件按相容的且有良好确定性的方式演化而来的。从此边界线以后的初始条件做相容的演化则问题浪多;初始条件可能不得不受限制,或者在不同的时间规定出限制。
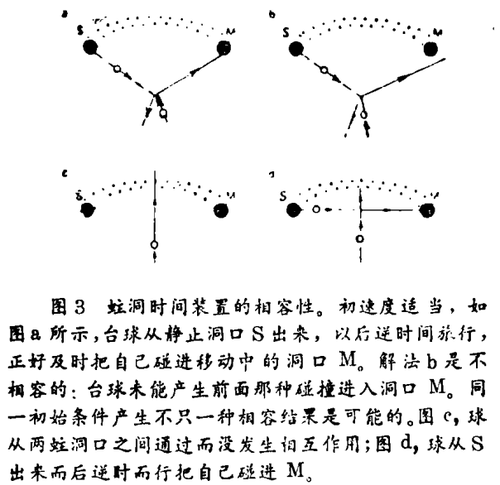
相互作用的系统情况更复杂,可以用蛀洞时空中“台球”的碰撞问题做说明。相容性限制了可能的初始条件范围(见图3 a和b)。初速度适当,球能被碰进蛀洞,而且在逆时行进时能以一种相容的方式把自身碰进洞。初速度不适当,则从时间装置出来的球不能把自身碰进洞;因为相容性原理不容许。但还有更多的情况。某些初始条件包含不止一个截然不同的相容解,如图3的c和d。一个球能不受干扰地从两洞口之间穿过,或者它能够被折射进洞;逆时行进,便显示出折射的原因。这两种相容结果来自同样的初始条件。来自加利福尼亚理工学院和莫斯科的研究工作者按量子力学规律处理这种球以解决这种佯谬。就此而论,两种结果的发生具有某种概率,但这些球的概率分配按唯一且相容的方式演变。还有多得多的事情尚待理解,看来时间旅行在物理学上的道理似乎比人们想到的还要多。
尚待解决的第一位问题是蛀洞的构造。例如,理论证明,除非时空几何已允许在时间内旅行,否则你不能在一个光滑经典的、到处有明确的时间方向的时空中形成蛀洞。大多数理论工作者推测,在非常小的尺度上,时空几何起伏与量子不确定性相协调,产生细小蛀洞“泡沫”。很可能通过以某种方式扩大这些细小泡沫蛀洞当中的一个就能获得宏观蛀洞。只有在这虽,可通行蛀洞和时间装置才涉及另一种蛀洞——微观蛀洞——的物理学。
在1950年代后期,当时在普林斯顿大学的约翰 · 惠勒(John Wheeler)已经提出,基本粒子可能是由电场或其它场孔道穿过的微观蛀洞组成。虽然未能证明这是一种有用的描述,但从那以后,理论工作者已经认为,时空应该有蛀洞穿过,蛀洞尺度为量子力学引力效应尺度。这刚好接近“普朗克尺度”,大约为10-35米。在任何引力的量子理论中,这些蛀洞起重要作用。
1987年斯蒂芬 · 霍金在这方面得出某些具体结论:他的结果指出,这种蛀洞改善了量子力学并且以不可预见的方式改变了自然常数。1988年,哈佛大学的悉尼 · 科尔曼(Sidney Coleman)对霍金的结论提出争议,尽管不是他的计算,但他断定量子蛀洞实际上以戏剧性的方式固定了某些物理常数。其它理论工作者很快参加进去,有人支持科尔曼的结论,有人不同意他的结论,
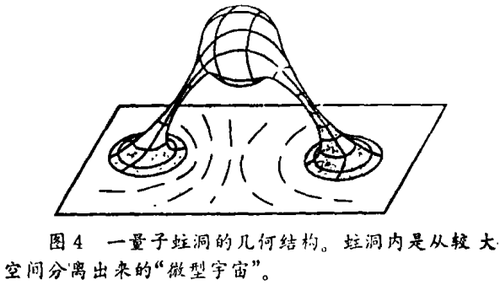
霍金认为,一种适当的万有引力的量子力学论述理应包含微观蛀洞几何结构的效应,如图4所示。这样一种几何结构代表一种“微型宇宙”(蛀洞内部)正在分出来并重新与较大宇宙相结合。他的计算认为,这些几何结构对物理进程的影响等效于基本粒子和微型宇宙之间简单的相互作用。他断定,这样一种相互作用会引起较大宇宙中量子系统的信息损失(落入蛀洞)。根据对所有可能的微型宇宙的固有状态做总计得知,这种相互作用也会造成用原来的理论描述基本粒子时得到的常数值漂移。这意味着,即使我们有综合性的“一切事物的理论”(“theory of everything”),它也是无用的。不首先做无数次测量以决定微型宇宙所引起的所有漂移,没有任何东西能算出来。
科尔曼的支持者对此有争议。他们争辩说,霍金的“信息损失”是无法观测到的。他们接转做了一个令许多人吃惊的结论:由微型宇宙造成的物理常数的漂移有可能解决长期存在的“宇宙常数问题”,及其它。
宇宙常数为爱因斯坦引力场方程一项的系数。可以把它理解为“真空中的能量密度”,当宇宙膨胀或收缩时此密度保持不变。(不同于物质或辐射,当宇宙体积改变时真空中不存在密集度的增加或减少;它保持着什么也没有)。爱因斯坦把宇宙常数引入他的方程为的是获捋描述宇宙的一个解,在1920年代末以前,人们相信宇宙充满物质,但是是静态的。爱因斯坦引用常数的理由后来已经不存在了——我们现在知道宇宙正在膨胀——而且观测证明宇宙常数非常小,或等于零,但理论工作者为摆脱它正遇到麻烦。
基本粒子物理预言真空能量是由于量子起伏产生的,像前面提到的卡西米尔能量一样。总能量密度一般比观测到的高120个数量级,为了使其协调,理论工作者需要把不同类型粒子的影响互相抵消到小数点后边120位(可能性不大)或者找到别的途径以摆脱宇宙常数。1984年霍金提出,量子引力可以做到这一点;科尔曼通过援引蛀洞的效应把此概念置于比较坚实的基础之上。
蛀洞所起的作用在引力的量子描述中叫做“历史的总和”(“sum-over-histories”)。这里给出的物理过程的几率;要计及能产生物理过程的所有可能“通路”。科尔曼认为,如果你在量子引力中以“历史的总和”的方式考虑微观蛀洞的影响,量子引力完全受历史控制,像我们自己的宇宙一样的大范围宇宙中,宇宙常数就要是零。因此,我们所做的任何测量宇宙常数的物理观测,其结果必定为零。此外,完全居支配地位的历史是这样的历史,牛顿万有引力常数,以及其它物理量大体上能取为最小值的历史。这需要确定所有微型宇宙的内部状态——物理常数所有的雷金漂移——从而确定所有的那些自然常数值。科尔曼把这种做法称为“大难题”是不足为奇的。
量子引力可能有这种戏剧性的效应,以及有可能加以计算,这种可能性把许多理论工作者吸引到这种课题上来。在过去两年里,它已成为活动温床。原始计算的许多变种,以及新的计算,已经发表——试验已作出的假设的有效性,极详尽地检验蛀洞的特殊模式,式寻找特殊的可观测效应。
然而,科尔曼和其它人的论证有缺点,有可能使他们所有的结论报废。对科尔曼采周的“历史的总和”所做的某些精心计算表明,具有零宇宙常数的那些历史并不像他声称的那样居支配地位,而是实际上受压制的。这样便不能确保基本上接近科尔曼、霍金和其它人已采用的,有明确定义的量子引力。英国哥伦比亚大学的威廉 · 昂鲁(William Unruh)沿这条路线已找到特别起破坏作用的结果。他断言,科尔曼和雷金在他们的求和中遗漏了整个一类历史;其中包括求和时忘了对任何物理过程做有限的预测。如果昂鲁是正确的,那么在这种探索中微观蛀洞就成了一种归谬法。(它具有和解决宇宙常数问题差不多的意义。但它不是大多数物理学家喜欢的那种结果)。
即使科尔曼的计算是正确的,当和观测相比较时理论仍可能失败。如果理论迫使牛顿常数具有的最小值是零或负值,那是办不到的。新近的结果也提到预测基本粒子质量的理论与其测量值有重大不一致,否则时空中蛀洞的密度就太大了,以致与众所周知的粒子物理相抵触。
争论并不是多余的。微观蛀洞可能使我们对量子引力的认识有突破性进展,它们也可能使我们现有的模式完全作废,证明这是一条死胡同。
不曾有一个人观察到蛀洞,不管是大的还是小的。所有我描述的这些都是理论的延伸,在经典情况下理由很充足,在量子情况下理由就不那么足。希望从事这两方面工作的每一位物理学家都能从实验工作者和观测人员所能提供的那些构思中找到其物理意义。
[New Scientist,1990年4月28日]